ارزش‌گذاری با مدل تنزیل سود نقدی سهام (DDM) به چه صورت است؟

مقاله پیش رو به یکی از مدل‌های ارزش‌گذاری سهام شرکت‌ها به نام «مدل تنزیل سود نقدی سهام» پرداخته است. در دنیای گسترده و پویای مالی، سرمایه‌گذاران به طور مداوم به دنبال روش‌های قابل اعتماد برای ارزیابی ارزش واقعی سهام و ارزش‌گذاری آن هستند. روش‌های ارزش‌گذاری به دو دسته شامل روش‌های نسبی و روش‌های مطلق تقسیم می‌شوند. در روش‌های نسبی، تحلیلگران با استفاده نسبت‌هایی نظیر p/e، p/s و p/b ارزش ذاتی سهام را محاسبه می‌کنند. در روش‌های مطلق اما بر اساس سه رویکرد ارزش‌گذاری خالص ارزش دارایی‌ها (NAV)، تنزیل سود نقدی (DDM) و تنزیل جریانات نقدی (DCF) ارزش ذاتی سهام برآورد می‌شود. در میان این مدل‌ها، مدل تنزیل سود سهام (DDM) به‌عنوان ابزاری برای تخمین ارزش ذاتی سهام بر اساس سود سهام مورد انتظار آتی آن‌ها، استفاده می‌شود. سرمایه‌گذاران می‌توانند با بررسی مدل DDM، درک عمیق‌تری از سازوکار آن شرکت به دست آورند و از پتانسیل آن برای اتخاذ تصمیمات سرمایه‌گذاری آگاهانه استفاده کنند. هدف این مقاله، بررسی مدل ارزش‌گذاری DDM، اصول اساسی، کاربردهای عملی و محدودیت‌های آن است.

ارزش‌گذاری تنزیل سود سهام (DDM) چیست؟

DDM که مخفف Dividend discount model است، به‌عنوان یکی از روش های ارزش‌ گذاری مطلق سهام شناخته می‌شود. تئوری مالی بیان می‌کند که ارزش یک سهم، ارزش تمام جریان‌های نقدی آتی است که با یک نرخ تنزیل، تعدیل شده است. از سود سهام تقسیمی می‌توان برای اندازه‌گیری جریان‌های نقدی برگشتی به سهامدار استفاده کرد. نکته مهمی که باید در نظر داشت، این است که زمانی می‌توان از این روش استفاده کرد که شرکت‌ها سودآور بوده و سیاست‌های شرکت به نحوی باشد که سالانه و مداوم سودی را میان سهامداران تقسیم کنند.

اجزای اصلی مدل ارزش‌گذاری تنزیل سود نقدی سهام (DDM)

برای درک DDM، دانستن اجزای اصلی آن ضروری است که در ادامه توضیح داده شده است:

سود سهام تقسیمی (DPS): سود نقدی سهام از اصلی‌ترین اجزای DDM است. در حقیقت سود سهام، پرداخت‌های نقدی انجام شده توسط یک شرکت به سهامداران خود است که به‌عنوان سود تقسیمی یا توزیعی نیز شناخته می‌شود. DDM هم سود سهام فعلی و هم سود سهام مورد انتظار آینده را در نظر می‌گیرد. برآورد سود سهام آتی مستلزم تحلیل دقیق پرداخت‌های سود سهام، نرخ رشد و سیاست‌های سود سهام شرکت است.

نرخ بازده مورد نیاز (Required Rate of Return): نرخ بازده مورد نیاز (Required Rate of Return)، حداقل بازدهی است که سرمایه‌گذاران انتظار دارند برای تحمل ریسک سرمایه‌گذاری در یک سهام خاص دریافت کنند. عواملی مانند نرخ بدون ریسک، ریسک سیستماتیک شرکت (بتا) که نوسانات یک اوراق بهادار یا پرتفوی در مقایسه با کل بازار را اندازه می‌گیرد و صرف ریسک سهام که یک پیش‌بینی بلندمدت از عملکرد بهتر بازار سهام نسبت به ابزارهای بدهی بدون ریسک است، را در نظر می‌گیرد. نرخ بازده مورد نیاز به‌عنوان نرخ تنزیل در DDM عمل ‌می‌کند و هزینه فرصت سرمایه‌گذاری در سهام را نشان می‌دهد. (RRR) حداقل مقدار سود (بازدهی) است که یک سرمایه‌گذار برای پذیرفتن ریسک سرمایه‌گذاری در سهام یا نوع دیگری از اوراق بهادار دنبال یا دریافت ‌می‌کند.

• جهت یادگیری بیشتر با این مباحث مطالعه مقاله آموزش تحلیل بنیادی پیشنهاد می‌شود.

چه زمانی از ارزش‌گذاری به روش DDM استفاده می‌شود؟

روش DDM بر این فرض است که ارزش ذاتی یک سهم تابع مستقیم جریان‌های نقدی مورد انتظار آن سهم در آینده است. این روش زمانی مورد استفاده قرار می‌گیرد که:

• پیش‌بینی می‌شود سود تقسیمی سهام ثابت و قابل اعتماد باشد
• سود تقسیمی سهام با نرخ ثابتی به طور نامحدود رشد می‌کند
• شرکت‌ها به طور مداوم سود سهام پرداخت می‌کنند
• در سیاست‌های شرکت امکان تغییر یا عدم پرداخت سود سهام وجود نداشته باشد

انواع مدل‌های DDM

در مدل DDM، ارزش فعلی کل سود پرداختی توسط شرکت در آینده محاسبه می‌شود. بر اساس این مدل، برای محاسبه ارزش سهام، سود نقدی آتی تنزیل شده و به زمان حال آورده می‌شود؛ در واقع می‌توان گفت ارزش فعلی سهام برابر با مجموع سود نقدی تنزیل شده آتی در نظر گرفته می‌شود. اگر ارزش به دست آمده از این روش بیشتر از قیمت معاملاتی فعلی سهام باشد، به این معنی است که سهام کمتر از ارزش واقعی خود قیمت‌گذاری شده‌ و واجد شرایط خرید است و اگر ارزش به دست آمده کمتر از قیمت فعلی سهام باشد، به این معنی است که سهام بیش از ارزش واقعی آن قیمت‌گذاری شده است و موقعیت فروش ایجاد می‌شود.

اکنون که اساس مدل تنزیل سود سهام (DDM) درک شد، می‌توان گفت که مدل تنزیل سود تقسیمی (DDM) بسته به اینکه پایان نگهداری دارایی همچون سهام مشخص یا نامحدود باشد، به روش‌های ذیل دسته‌بندی می‌شود:

1. مدل تنزیل سود سهام یک دوره‌ای
2. مدل تنزیل سود سهام چند دوره‌ای
3. مدل رشد گوردون
4. مدل تنزیل سود سهام دو مرحله‌ای
5. مدل تنزیل سود سهام H
6. مدل تنزیل سود سهام سه مرحله‌ای

در ادامه به جزئیات هر یک از مدل‌ها به‌صورت کامل پرداخته شده است:

مدل تنزیل سود سهام یک دوره‌ای

مدل سود تقسیمی سهام یک دوره‌ای زمانی به کار گرفته می‌شود که سرمایه‌گذار بخواهد قیمت ذاتی سهامی را که در یک دوره آینده (معمولا یک سال از هم اکنون)، به فروش می‌رساند، تعیین کند. مدل یک دوره‌ای فرض می‌کند که یک سرمایه‌گذار قصد دارد که سهام را تنها برای یک سال مالی نگه دارد. بنابراین، برای تعیین قیمت منصفانه سهام، مجموع سود پرداختی آتی و قیمت فروش تخمینی باید محاسبه و به ارزش فعلی تنزیل شود.

مدل سود تقسیمی سهام یک دوره‌ای از طریق فرمول زیر محاسبه می‌شود:

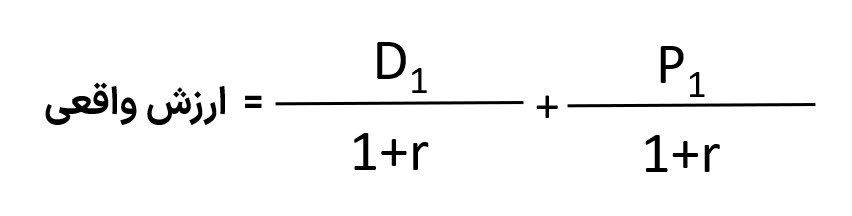
D = سود تقسیمی

P = قیمت تخمینی سهام در یک دوره آینده

r = نرخ تنزیل

مدل تنزیل سود سهام چند دوره‌ای

مدل تنزیل سود تقسیمی سهام چند دوره‌ای در واقع مدل توسعه یافته تنزیل سود تقسیمی سهام یک دوره‌ای است که در آن سرمایه‌گذار انتظار دارد، سهام را برای دوره‌های متعدد نگه دارد. چالش اصلی این مدل، پیش‌بینی سود تقسیمی سهام برای دوره‌های مختلف در آینده است. در DDM چند دوره‌ای، یک سرمایه‌گذار انتظار دارد سهامی را که خریداری کرده برای دوره‌های زمانی متعدد نگه دارد. بنابراین، جریان‌های نقدی مورد انتظار آتی شامل پرداخت‌های سود سهام متعدد و قیمت فروش تخمینی سهام در پایان دوره نگهداری خواهد بود.

ارزش ذاتی یک سهام (از طریق DDM چند دوره‌ای) با تخمین مجموع ارزش سود تقسیمی مورد انتظار طی دوره‌های آتی و در نهایت تنزیل قیمت فروش به دست می‌آید. فرمول ریاضی مدل به شرح زیر است:

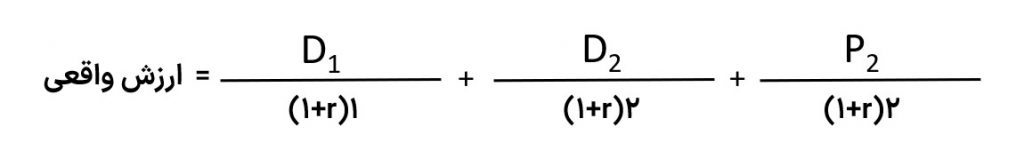
مدل رشد گوردون (Gordon Growth Model)

مدل تنزیل سود رشد گوردون (GGM) به افتخار مایرون جی.گوردون از دانشگاه تورنتو نام‌گذاری شد و از آن به‌عنوان مدل رشد دائمی ثابت نیز یاد می‌شود.این مدل یکی از متداول‌ترین مدل‌ها در ارزش‌گذاری است. GGM بر این فرض استوار است که جریان سود تقسیمی سهام در آینده با نرخ ثابتی و برای مدت نامحدودی رشد خواهد کرد. از این مدل برای ارزیابی ارزش کسب‌وکارهای پایدار با جریان نقدی قوی و نرخ رشد ثابت استفاده می‌شود. به طور کلی فرض می‌شود که شرکت مورد ارزیابی دارای یک مدل تجاری ثابت و باثبات است و رشد شرکت با نرخ ثابتی در طول زمان اتفاق می‌افتد.

فرمول این مدل به‌صورت زیر است:

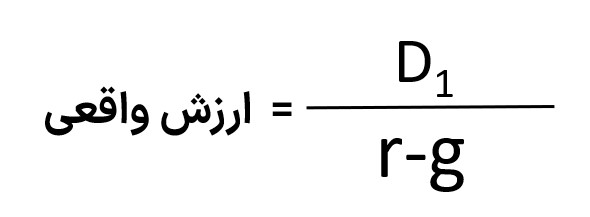
D = سود تقسیمی

r = نرخ تنزیل

g = نرخ رشد ثابت سود سهام شرکت برای مدت نامحدود

مدل تنزیل سود سهام دو مرحله‌ای

این مدل شامل دو بخش است و فرض می‌کند که سود سهام دو مرحله رشد را طی می‌کند. در مرحله اول، سود سهام با نرخ ثابتی برای مدت زمان مشخصی رشد و در مرحله دوم، فرض بر این است که سود سهام با نرخ متفاوتی برای باقیمانده عمر شرکت رشد می‌کند. به این ترتیب، بخش دوم مدل دو مرحله‌ای اساسا با مدل رشد گوردون یکسان است، بنابراین درک دقیق فرمول گوردون که در بالا تشریح شد، به افراد کمک می‌کند تا این مدل و سایر فرمول‌های پیچیده‌تر را بهتر درک کنند.

مدل دو مرحله‌ای اغلب برای تعیین ارزش ذاتی سهام منتشر شده توسط شرکتی که در حال توسعه و گسترش سریع است، استفاده می‌شود. شرکت‌های جدیدتری که ماندگاری خود را ثابت کرده‌اند اما هنوز در مرحله اولیه رشد سریع هستند، موردهای خوبی برای این روش ارزش‌گذاری هستند. مرحله اول رشد دو مرحله‌ای سود سهام عموما کاملا تهاجمی فرض می‌شود که نشان‌دهنده توسعه سریع شرکت است، در حالی که مرحله دوم نرخ پایین‌تر و پایدارتر رشد سود سهام را در نظر می‌گیرد. فرمول این روش در ادامه آورده شده است:

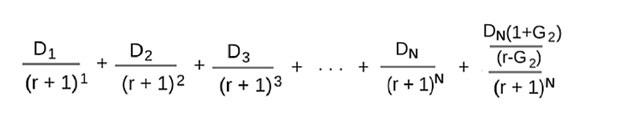
D1= سود تقسیمی یک سال بعد (الباقی هم برای سال‌های دوم و سوم است)

r = نرخ تنزیل

G₂ = نرخ رشد متغیر (مرحله دوم)

N = تعدادسال

مدل تنزیل سود سهام H

مدل تنزیل سود سهام مدل H مانند مدل دو مرحله‌ای است که ارزش ذاتی فعلی سهام را در دو مرحله کلیدی محاسبه می‌کند. با این حال، در حالی که مدل دو مرحله‌ای فرض می‌کند که سود سهام با یک نرخ ثابت رشد می‌کند و سپس به طور ناگهانی نرخ رشد برای آینده کاهش می‌یابد، مدل H بیانگر تغییر تدریجی در نرخ رشد در طول زمان را نشان می‌دهد.

در مرحله اول محاسبه مدل H، فرض بر این است که سود سهام در هر سال افزایش یا کاهش می‌یابد. به عنوان مثال، نرخ رشد سود سهام یک شرکت ممکن است به مدت سه سال هر سال 2٪ کاهش یابد تا فرضا از 15٪ به 9٪ برسد. در این‌جا نرخ تغییر عددی ثابت و برابر با ۲ درصد است اما خود نرخ رشد به تدریج کاهش می‌یابد. مرحله دوم مدل H با مدل دو مرحله‌ای یا مدل رشد گوردون یکسان است. در مرحله اول، نرخ رشد به آرامی تغییر می‌کند تا زمانی که در یک نرخ رشد ثابت شود.

در مثال بالا، فرض می‌شود که در سال چهارم نرخ رشد سود سهام به 7 درصد کاهش می‌یابد و در این نقطه تثبیت شود. در این حالت در ادامه از فرمول مدل رشد گوردون می‌توان برای محاسبه ارزش فعلی تمام سود سهام آتی بر اساس این افزایش پایدار 7 درصدی در سال استفاده کرد. فرمول این روش در ادامه آورده شده است:

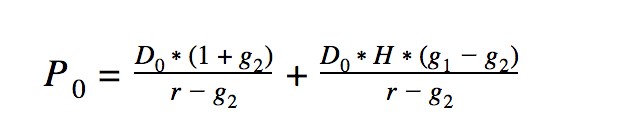
D0= سود تقسیمی سال جاری

r = نرخ تنزیل

G₁ = نرخ رشد اولیه

G₂ = نرخ رشد پایانی

H = نرخ ثابت تغییر

مدل تنزیل سود سهام سه مرحله‌ای

مدل تنزیل سود تقسیمی سهام سه مرحله‌ای بسیار شبیه مدل‌های قبلی همچون مدل رشد گوردون، مدل دو مرحله‌ای و مدل H است. در واقع، اساسا ترکیبی از این سه مدل است که هدف آن حذف برخی از کاستی‌های این فرمول‌ها است.

مدل رشد گوردون اساس همه فرمول‌های تنزیل سود سهام تقسیمی است، اما سادگی ذاتی آن به این معنی است که دقت بالایی ندارد، چرا که فرض می‌کند که سود سهام با نرخ ثابتی برای همیشه رشد می‌کند. هر دو مدل دو مرحله‌ای و مدل H امکان تغییر نرخ رشد سود سهام را فراهم می‌کند، اما تنها مدل H به جای تغییر شدید از یک نرخ ثابت به نرخ دیگر، تغییرات افزایشی را امکان‌پذیر می‌کند. مدل سه مرحله‌ای عناصر هر سه مدل را در بر می‌گیرد، یک دوره اولیه رشد بسیار شدید یا اندک و به دنبال آن یک دوره افزایش یا کاهش تدریجی که در نهایت در نرخ رشد متوسط ​‌تری تثبیت می‌شود و فرض می‌شود این نرخ رشد در تمام عمر شرکت ادامه خواهد داشت. فرمول این روش در ادامه آورده شده است:

D1= سود تقسیمی سال اول

r = نرخ تنزیل

G₁ = نرخ رشد اولیه

G₂ = نرخ رشد پایانی یا پایدار

H = نرخ ثابت تغییر

N = تعدادسال

محدودیت‌ها و معایب مدل ارزش‌گذاری به روش DDM

روش DDM به رغم آنکه برای درک بهتر ارزش ذاتی سهام شرکت‌ها به ویژه شرکت‌هایی که سود تقسیمی پایدار دارند، بسیار کمک‌کننده است، اما دارای برخی اشکالات است که در ادامه به آن پرداخته شده است:

حساس به مفروضات: تغییرات کوچک در مفروضاتی همچون نرخ تنزیل یا تخمین‌های نرخ رشد به طور چشم‌گیری منجر به نوسان ارزش واقعی سهام یک شرکت می‌شود. 

خطای پیش‌بینی: پیش‌بینی دقیق سود تقسیمی سهام در بلندمدت عملا غیرممکن است. بنابراین هرگونه خطا در پیش‌بینی نتایج را تغییر می‌دهد.

عدم دقت به متغیرهای بیرونی: ارزش‌گذاری به روش DDM در واقع تغییر در استراتژی آینده یک شرکت، تغییرات اقتصادی یا ریسک‌های سیستماتیک را در نظر نمی‌گیرد.

عدم امکان سرمایه‌گذاری مجدد: این روش ارزش ایجاد شده از سرمایه‌گذاری مجدد سود در شرکت‌های با رشد بالا را نادیده می‌گیرد.

نامناسب برای شرکت‌هایی با تقسیم سود محدود یا بدون تقسیم سود: این روش برای ارزش‌گذاری شرکت‌هایی با سود سهام محدود یا بدون سود بسیار دشوار است.

در اولویت قرارگرفتن سود سهام: این روش به پرداخت‌کنندگان سود سهام نسبت به شرکت‌هایی که مسئولانه درآمد را حفظ و مجددا آن را سرمایه‌گذاری می‌کنند، بهای بیشتری می‌دهد.

ارزش‌گذاری به روش DDM قابل اتکا است؟

مدل تنزیل سود تقسیمی با این فرض ایجاد شده که ارزش ذاتی یک سهام منعکس‌کننده ارزش فعلی تمام جریان‌های نقدی آتی ایجاد شده توسط یک اوراق بهادار همچون سهام است. سود سهام تقسیمی در واقع جریان‌های نقدی مثبتی است که توسط یک شرکت تولید می‌شود و میان سهامداران توزیع می‌شود.

به طور کلی، مدل تنزیل سود یک روشی آسان برای محاسبه قیمت منصفانه سهام با استفاده از فرمول‌های ریاضی و حداقل متغیرهای ورودی مورد نیاز ارائه می‌کند. با این حال، مدل‌های آن متکی بر چندین فرضیه است که نمی‌توان براساس آن به راحتی پیش‌بینی کرد.

بسته به تنوع مدل تنزیل سود، یک تحلیلگر نیاز به پیش‌بینی سود تقسیمی سهام در آینده و نرخ رشد آتی آن و نرخ تنزیل (هزینه سرمایه) دارد. پیش‌بینی دقیق همه متغیرها تقریبا غیرممکن است. بنابراین، در بسیاری از موارد، قیمت منصفانه سهام از نظر تئوری با واقعیت فاصله دارد. بنابراین استفاده از این روش به تنهایی قابل اتکا نیست.

سخن آخر

مدل تنزیل سود سهام (DDM) یک رویکرد سیستماتیک را جهت برآورد ارزش ذاتی یک سهام بر اساس سود سهام مورد انتظار در آینده به سرمایه‌گذاران ارائه می‌دهد. با درک مکانیزم DDM و اجزای آن، سرمایه‌گذاران می‌توانند بینش ارزشمندی در مورد عواملی که قیمت سهام را افزایش می‌دهند، به دست آورند. اگرچه DDM محدودیت‌های خود را دارد، اما در صورت استفاده مناسب، ابزاری قدرتمند در ارزش‎‌گذاری سهام است. با ترکیب مفاهیم DDM، سرمایه‌گذاران می‌توانند اثربخشی آن را افزایش دهند و تصمیمات آگاهانه‌تری جهت سرمایه‌گذاری اتخاذ کنند.

در نهایت، DDM به‌عنوان یک چارچوب ارزشمند برای ارزیابی ارزش واقعی سهام و شناسایی فرصت‌های بالقوه در دنیای پویای مالی عمل می‌کند. این مدل تاکید می‌کند که ارزش سهام از ارزش فعلی سود آتی سهام آن مشتق می‌شود و رویکردی برای تخمین ارزش ذاتی سهام ارائه می‌کند و سرمایه‌گذاران را قادر می‌سازد تا ارزیابی کنند که آیا سهام در بازار ارزنده یا غیرارزنده هستند.